Vector Search General

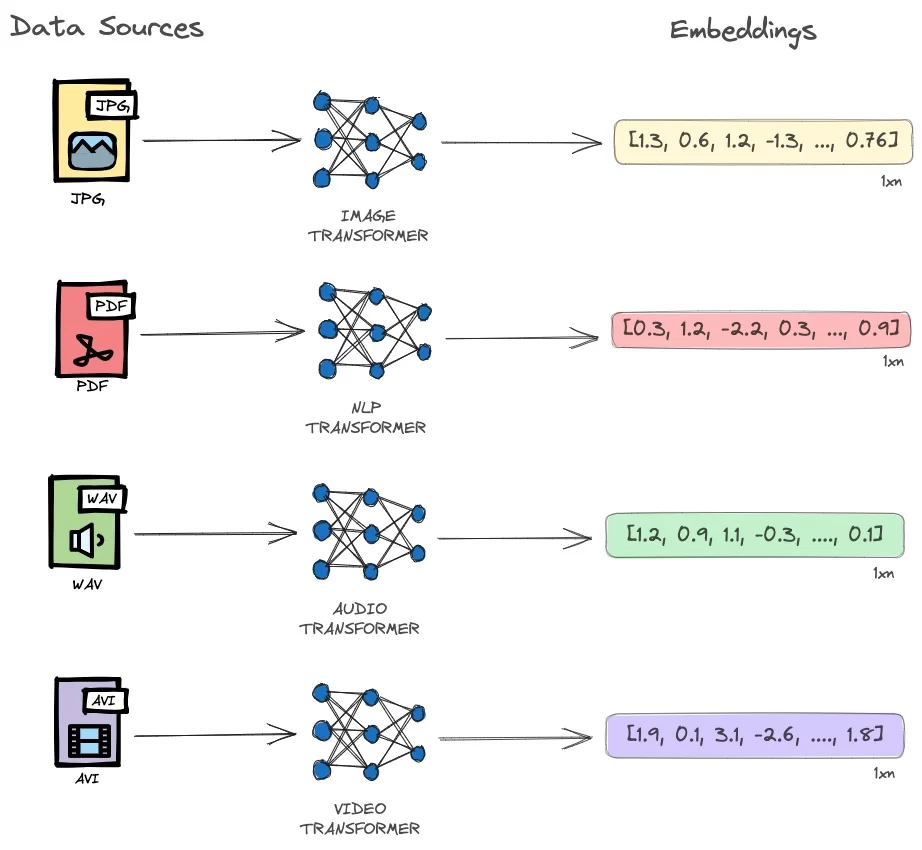
What is Data Vectorisation?

Vectors are encoded representations of unstructured data like text, images, and audio in the form of an ordered arrays of numbers (floats or int8).

Credit: CeVo Australia

These vectors are produced through machine learning techniques, carried out by “Embedding Models”. Embedding models can be based on varying abstracted techniques, but the most commonly used models currently are Transformer models.

Embedding models/Transformers are developed through a various algorithms, architectures and concepts — but they generally will perform some kind of iterative “learning” on massive datasets.

• This stage usually involves unsupervised learning tasks, such as language modeling.
• As an example, models like BERT are trained using tasks like masked language modeling, where certain words in sentences are masked out, and the model learns to predict these missing words based on the context.

Through the “learning” of relationships/meanings between different data, Embedding models end up being able to effectively capture meaningful relationships and similarities between data.

This enables users to query data based on the semantic meaning rather than the literal data itself (such as by exact string matching) — this is the concept behind Vector Search.

What is Vector Search?

Vector Search refers to the ability to use vectors to determine the semantic similarity of various data points. In using vectors, input data sources can still have it’s “meaning” mapped and compared to other data sources though the use of embeddings.

Vector Databases are great for:

• Semantic understanding:
  • Capturing meaning and context to input, as opposed to simply searching for exact matches in patterns. This allows for nuanced matching (and ranking of similarity), as opposed to binary views of matching or not.
• Multi-modal capabilities:
  • By leveraging the multi-modal transformers to encode and decode information, functionality is often multi-modal and can interact based on their vector representations.
• Context-preservation
  • Much larger inputs can be referenced through referring to a vector, and hence context is not loss.
    • E.g traditional text search breaks strings into their individual words, whereas Vectors represent the entire chunk of text/data.
• Querying large datasets very quickly
  • Vector relationships are generated and structured during indexing time, not query time.
  • Hence, so long as the embeddings are created prior to searching, queries run-time scales very well with massive datasets.

How does it work? What is Vector Similarity?

Vector search refers to the utilisation of a query (often with the assistance of Natural Language Models), to find other vectors that are “similar”. This is vector similarity.

As concisely described by Jose Parra in this post:

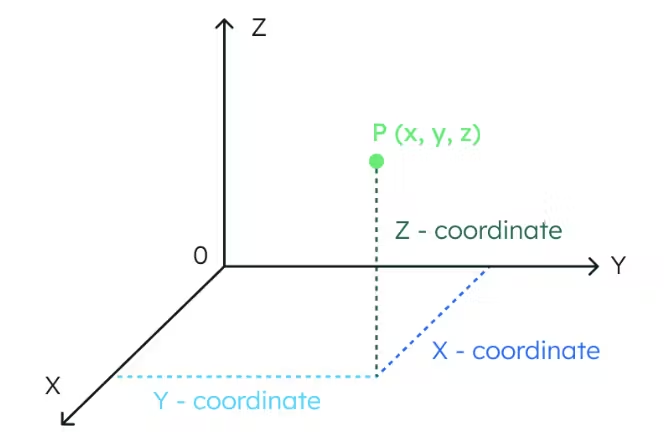
“To understand the concept of vector similarity, let’s picture a three-dimensional space. In this space, the location of a data point is fully determined by three coordinates.

In the same way, if a space has 1024 dimensions, it takes 1024 coordinates to locate a data point.”

To clarify on his latter point, each additional dimension will add a new element in the array. Hence, a vector with n amount of dimensions, has n amount of elements in the resulting embedding array.

• This is what is meant, when Vector Search is described as “operating in a multi-dimensional space”.
• A vector search will require a vector query to have the same amount of dimensions/embedding elements, as to complete a valid search — similar to valid use of coordinates.
• The lower the dimensions, the more data gets “crowded” due to overlapping locations. By adding dimensions, data has more space to sparsely spread out — in doing this, you can generally increase the precision of prompts.
• tl;dr the more dimensions, the more ability the machine has to separate concepts in a Vector Database.
  • The trade-off is that generally, more dimensionsionality means more compute is required for retrieval.

As data is plotted across different “coordinates” in this multi-dimensional space, we can use various mathematical concepts to determine “similarity”, depending on their “distance” relative to eachother.

Some of the more commonly used distance metrics used are:

• Euclidian Distance
• Cosine Similarity
• Dot Product
• Manhattan Distance

To read more on this, see my other note: Vector Search Retrieval and Distance Metrics.

---

Resources:

• Vector Search and LLM Essentials - What, When and Why | MongoDB
• Vector Similarity Explained | Pinecone
• Distance Metrics in Vector Search | Weaviate